We’re getting into a little bit of math today, which we’ll need to in order to understand some fundamentals in Unity; game development too. You may be tempted to skip this tutorial, but this is math that will be applicable to any game development you work with. Knowing how vectors work is super important!
There are other math structures that would be good to learn about, such as Quaternions and Matrices. However, we don’t need an in depth knowledge to get started, so for now we’ll leave them on the side lines.
Generally Speaking
Vectors in the most literal sense are values representing two main components: a direction and a length/magnitude). They can be used for lots of different cases, but ultimately they are made up of those two pieces. To start off, we’re going to look at 2D vectors, as to not get too complicated, then we’ll apply that to 3D.
Vectors in 2D
Think back to your younger years of education, where you may have learned about graphs and plotting coordinates. We can look at vectors in a very similar way. Let’s say we have two points setup here.
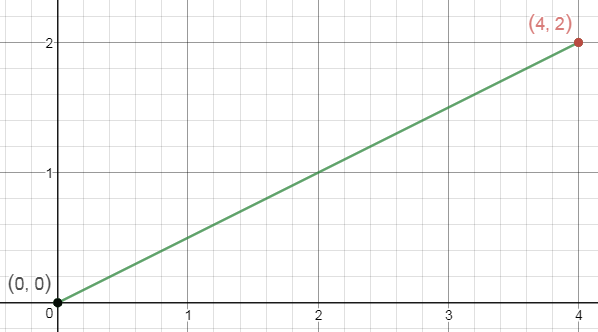
Now if we wanted to get the slope between these points we’d use the slope formula, which is simply (Y2 – Y1) / (X2 – X1). Which is simply get ting the difference between the X and Y points to figure out how far we have to move from our origin point to get to the destination.
In this example, since our origin point is (0, 0), that’s super simple. (2 - 0) / (4 - 0) is simply 2/4. Reading this, it just means we go up two points, and to the right 4 points.
This might seem like simple math, but this is the basis of a vector. To get the vector from these two values it’s nearly identical: (Y2 - Y1, X2 - X1) it’s just in a different format, so instead of a fraction it’s shown in the (X, Y) format as a vector. When writing out a vector in notation, we write it as $latex \overrightarrow{A}$ where A is our vector. So in this example it would be written as $latex \overrightarrow{(4, 2)}$
Take a look at another example without an easy origin of 0,0.
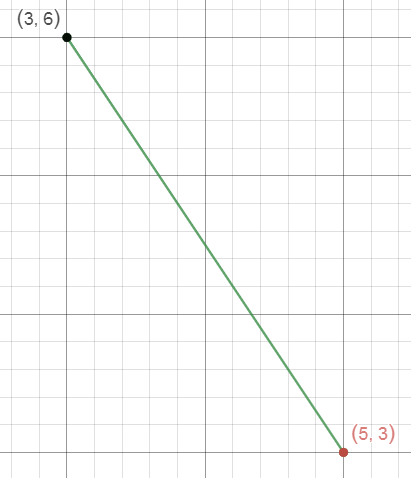
In this case there will be negative values, because our direction will be downwards. Order is important, it determines which direction it actually represents. You could be going down and to the right, or up and to the left. Do this problem yourself and you can check your answer here.
Okay, So What?
That might’ve seemed easy, but now let’s look into more specific vector information. There are several pieces of information we may want to know about a single vector, it’s length, it’s direction, etc. Lets check out how we might find those.
Length/Magnitude
You will find it useful to get the length (also know as magnitude) of a vector quite often. You’ll often see this shown as $latex \left \| \overrightarrow{A} \right \|$ in notation where A is a vector. We use this formula, which is as follows:
$latex \sqrt{X^2 + Y^2}&s=3$
Then, you can just plug in the numbers. Let’s take the example vector $latex \overrightarrow{(5, 8)}$, and just plug this into the formula it breaks down as the following:
$latex \sqrt{5^2 + 8^2}&s=3$
$latex \sqrt{25 + 64}&s=3$
$latex \sqrt{89}&s=3$
~9.43
This gives us useful information about how long our vector is, and we can use this to get other information too, including getting the normalized direction.
Normalized Direction
There are many cases we want to focus on the direction we’re traveling and not the distance, but our vector having a distance becomes a problem. Such as if we had a character who needs to move in a direction at a certain speed, that distance will affect the speed.
So what we need is to normalize the direction, which makes the vector magnitude equivalent to 1. This way when we multiply our speed, it will always be the speed we need, and not affected by the length between the two points. Getting the vector normalized is also known as a unit vector.
So to do this, the formula is very simple:
$latex \frac{\overrightarrow{A}}{\left \| \overrightarrow{A} \right \|}&s=3$
We simply divide our vector by the magnitude of our vector. So using our previous example and answer ($latex \overrightarrow{(5, 8)}$ and ~9.43) we can just plug them in.
$latex \frac{\overrightarrow{(5, 8)}}{9.43}&s=3$
This results in $latex \overrightarrow{(0.53, 0.84)}$, which you’ll notice is very small. Unit vectors will always be between -1 and 1, which will make it perfect for just representing a direction.
Operations
Besides those, there are a lot of general operations you can apply, just like most numbers.
Scalars
Scalars being extremely useful, they’re used to just increase a vectors magnitude by a certain scalar amount. Realize, scalar is really just a word for a float number value to increase another value. If you have a vector of $latex \overrightarrow{(2, 3)}$, you can scale it by 3 to get $latex \overrightarrow{(2, 3)} * 3 = \overrightarrow{(6, 9)}$
You can also use this to change a unit vector back to its original magnitude. Taking the example we had above, the result we got was $latex \overrightarrow{(0.53, 0.84)}$, now multiply that by its magnitude of ~9.43. We get the original vector $latex \overrightarrow{(5, 8)}$.
Addition & Subtraction
You can add and subtract vectors, which operates pretty much how you would expect. For addition it’s simply (A.x + B.x, A.y + B.y), subtraction is (A.x – B.x, A.y – B.y). Note, this works between vectors, but not scalars. You can not do $latex \overrightarrow{A} + 5$, this is not a supported operation, you would have to add another vector.
This can be helpful in a variety of cases. For example, if you had an enemy and your player, and you wanted to get the direction from your enemy to the player you could find this with subtraction. Subtract the players position with the enemies, take that vector and normalize it. This yields the direction from the enemy to the player.
Normalize(PlayerPosition - EnemyPosition)
Dot Product
The dot product is extremely useful in a variety of scenarios, especially in game development. It can compare two vectors, and return a float scalar value representing the angular relationship between the two. We’ll go into this more in a second.
There are actually two formulas you can use for the dot product:
$latex \left \| \overrightarrow{A} \right \| * \left \| \overrightarrow{B} \right \| * \cos(\theta)&s=2$
OR
$latex \overrightarrow{A}.x * \overrightarrow{B}.x + \overrightarrow{A}.y * \overrightarrow{B}.y&s=2$
There are a lot of mathematical explanations for how and why these work, and what exactly they mean online. I won’t be covering that, but rather what it can mean to you and how you might use it.
It is best to use unit vectors when comparing your two vectors. The result you’ll get from the dot product will be between -1 to 1. This result determines how the angles of these two vectors are related. There are 3 main results you can get from this information.
- If the result is 0, that means these vectors are perfectly perpendicular.

- If the result is positive, this means the directions are closer to being in the same direction, below $latex 90^{\circ}$. This can tell you how close two vectors are to facing the same direction, the closer to 1 the more similar they are. At 1 they’re the same.

- If the result is negative, this means the directions are facing further away from each other. Where they are greater than $latex 90^{\circ}$ away from one another. This can tell you if two vectors are facing away from each other. At -1, they’re exactly opposite.

This kind of information can be incredibly useful for lots of cases. Think of a single case of AI for example, comparing their facing direction to the direction of the player can tell you if they’re facing the player or facing away from them.
Now you’ve seen how 2D vectors work, we’ve seen the equations how they relate on a X, Y coordinate plane. Let’s take a look at adding another axis.
3D Vectors
Don’t be afraid adventurer, while one extra axis does increase the complexity of some things, everything you’ve learned is still relevant. Up to this point we’ve just had to deal with the X and Y. Now we want to visualize this in 3d, with a Z that goes away/towards the screen.
Left Handed vs Right Handed
There are actually two different coordinate systems we have to look at. This basically determines if the positive Z values are heading towards or away from us, into the screen or out of it.
A left handed system the Z is positive heading away from the screen, while the right hand is the opposite. There’s a good simple demonstration of that here. For example, in this image we’re using a right-handed system.

2D to 3D Operations
Now, all the operations we went over before are still relevant. They’re nearly exactly the same, except we add one more axis.
Magnitude: $latex \sqrt{X^2 + Y^2 + Z^2}&s=3$
Normalization: $latex \frac{\overrightarrow{A}}{\left \| \overrightarrow{A} \right \|}&s=3$ (Exactly the same)
Dot Product: $latex \overrightarrow{A}.x * \overrightarrow{B}.x + \overrightarrow{A}.y * \overrightarrow{B}.y + \overrightarrow{A}.z * \overrightarrow{B}.z&s=2$
All of these functions work the same way, you just add the axis onto what already exists.
Cross Product
Now the cross product is a useful formula that is used with 3D vectors. Comparing two 3D vectors, you’ll have a plane, and it will return a new vector coming out of that plane in the positive Z axis.
So let’s look at this, we have two vectors, as they cross each other you can see they make a plane.
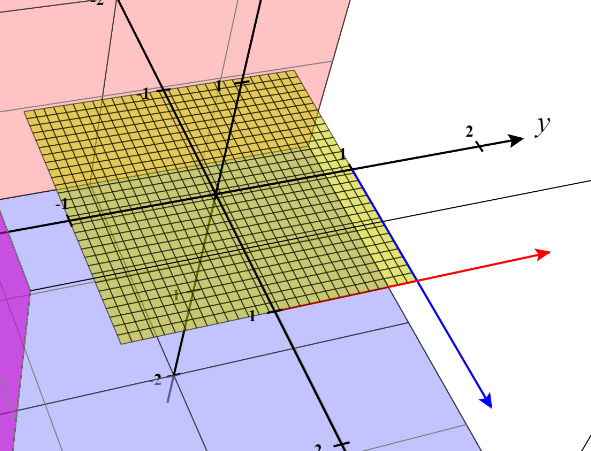
Here, doing the cross product will result in this green vector.

The math for the cross product is a bit tedious, but not complicated.
$latex X = \overrightarrow{A}.y * \overrightarrow{B}.z – \overrightarrow{A}.z * \overrightarrow{B}.y&s=2$
$latex Y = \overrightarrow{A}.z * \overrightarrow{B}.x – \overrightarrow{A}.x * \overrightarrow{B}.z&s=2$
$latex Z = \overrightarrow{A}.x * \overrightarrow{B}.y – \overrightarrow{A}.y * \overrightarrow{B}.x&s=2$
Then just combine those into our vector of $latex \overrightarrow{(X, Y, Z)}$
Unity
Soon you’ll be heading into Unity, and knowing how to use a vector, and how it functions will be useful. Most of these functions are thankfully already written for you, you’ll be able to just use Vector3.Dot() instead of doing the math yourself. Hopefully this has given you some insight into how vectors work and what they represent.
Support
Are you having trouble with understanding this tutorial? Please feel free to contact me via email at KoseckCory@gmail.com or message me on discord at 7ark#8194.
I would love to get feedback from people so I can add and improve these tutorials overtime. Letting me know what you’re confused about will let me update the tutorials to be more concise and helpful.
If you’re interested in supporting me personally, you can follow me on Twitter or Instagram. If you want to support me financially, I have a Patreon and a Ko-fi.


0 comments on “Using Unity Preface: What Are Vectors?”Add yours →