I bet you can’t wait to take a byte out of this next tutorial, but it will take a bit to wrap your head around. We’ll be going into some of the complexities of your computer, entering the matrix to play around with 1s and 0s. Any further complicated subjects you should do some research into will be highlighted in bold.
What Are These Bits and Bytes?
I’m glad you asked. Bits are the 1s and 0s you’ll often hear about, they’re what make up the code of your computer. Together it’s all binary, and each of the 1s or 0s is named a bit.
Then you have bytes, which are made up of 8 bits. You could have 00000000 which is one byte of all 0 bits. We read things as a series of bytes. For example, an int consists of 4 bytes of data.
Powers
To understand how binary works, we need to look at how it’s setup. Let’s use a friendly example to get you started on the idea; decimal. You know decimals, it’s basically any number, 1, 50, 562, whatever. Decimals are more similar to binary than you think. Decimals use a power of 10, where binary uses a power of 2. Let’s look at an example to explain this.
Let’s say we’re looking at the number 1234. If we split this up into each tenth, we would have 1000, 200, 30, and 4. Those are each of the 10s spot, if we laid this out similar to binary, we would have something like this:
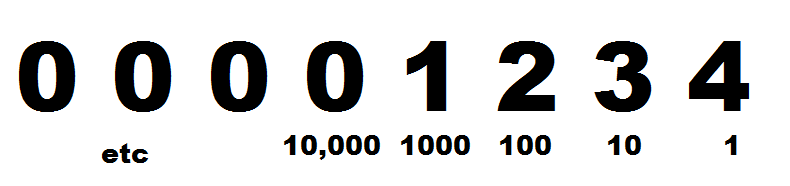
Here you can see each value with each power you would multiply by. From this, how do we get our result of 1234? Starting from the right, we take our 10 digit value (0 – 9) and multiply it by it’s 10 power place. Then we add each together.
In this case: 4 * 1 = 4 + (3 * 10) = 34 + (2 * 100) = 234 + (1 * 1000) = 1234. And then the rest are 0s, so they wouldn’t add anything. Binary works the same way just with a power of 2, instead of a possible 10 digits from 0 to 9, there are only two, 0 and 1.
Reading Binary
When you put these together we have binary, it can represent different numbers, letters, etc. Put together it’s how we run everything on our computers. We can manually look at a byte and decipher it’s value.
Just like reading a normal number as shown above, we’ll do the same thing here.
Each spot represents a different number value, that doubles from right to left. When the value is 0, that bit is off, and so it doesn’t contribute to the total value. Depending on what values you turn on and off, it adds to the value, and allows you to get any number up to 255 in a single byte by combining different bits.
If we had 00000101, we have the 1st and 3rd slot filled, which according to this diagram is 1 and 4. So that means the value of this byte is 5. We could convert this to ASCII, which is essentially just letters represented in their numerical format.
ASCII
For example, a byte value from 65 – 90 is the same as the capital letters of A – Z. The lowercase versions are 97(a) – 122(z). The other values aside from letters is made up of various symbols, like 32 is space, 48 – 57 is 0 – 10, etc. With this you could essentially make up your entire sentence out of binary; which is exactly what our computers use binary to do.
01000011 01100001 01101110 00100000 01111001 01101111 01110101 00100000 01110010 01100101 01100001 01100100 00100000 01110100 01101000 01101001 01110011 00111111
Bytes as Values
We understand now that a byte is made up of 8 bits, each adding to the total value. So now let’s look at these bytes in the context of programming and variables. A char in C# is one byte, because it simply represents one ASCII symbol; which as we just went over, is represented by one byte.
Little and Big Endian
There are two different ways bytes are formatted though, which is known as little or big endian style. It’s essentially like reading, and determines whether we read from left to right (big endian), or right to left (little endian). In general most things use little endian as a standard.
If we had the values 00001111 00110011 stored, these are two bytes of data. In little endian we start reading from the right side as the lowest value and it increases to the left; in big endian it’s the reverse. For this tutorial I’ll be explaining everything in little endian.
Int
What about when we have other variables that are more complicated? Well, those are made up of multiple bytes. This is the reason we have shorts, ints, and longs for example. Shorts are 2 bytes, ints are 4 bytes, and longs are 8 bytes; and these all let them hold lower or higher numbers based off of how much space we have. The min and max for these values also depends on if the value is signed, or unsigned.
Let’s look at a normal int-32. 32 representing how many bits it has, you may see short referred to as a int-16, and a long as a int-64. When we have multiple bytes in a row, the method we used to find the value of a single byte just keeps going. So where our last bit value had been 128, we keep going onto 256, 512, 1024, etc.
If we do this long enough, eventually the total value for 4 bytes is 4,294,967,295. That’s a big number. Now if you were to use int.MaxValue, and print that out to the console you might be confused. It will give you the value 2,147,483,647, which is about half of our value for 4 bytes.
Why is this? Well you should notice when you make an int variable that you can make the number negative, but our byte values don’t account for this. This is why we have both an int, and a uint. The uint stands for unsigned int, and if you used uint.MaxValue, that would return 4,294,967,295.
How do we take these negative values into account?
Negative Values
For simplicity, we’re going to use a byte as an example again. A negative byte goes from -128 to 127. For the positive values, it works the same all the way up to 127 (01111111). Then at any number that would normally be 128 – 255 is now a negative number, with 128(10000000) now being -128, and 129(10000001) now being -127, and so on. All the way down to -1 at 11111111.
Now if we have a positive number like 1, and we want to get the negated value of -1, there’s a formula to get that value.
Twos Compliment
There is a method known as two’s compliment for converting a positive byte value into a negative one. It’s pretty simple, you take your binary value (for 1 it would just be 00000001) and negate it. Which means taking all the 0s and changing them to 1s, and vise versa. So that would change this to 11111110. Now take that positive number, and add one. The positive value of this would be 254, adding one it’s 255. Change that back to binary and you have 11111111, which as we said earlier is equal to -1.
Casting
Now we’ve used casting in the past, changing between different values. Well when you’re changing from a value of some amount of bytes to another, it’s important to know what happens to them.
Let’s say you have a int value (remembering it’s 4 bytes) and it consists of 00000000 00000010 00001100 01100100 (which as a decimal is 134244). If we want to convert that int to a short (2 bytes), then we’re risking losing data, which is why C# forces you to cast it, so you acknowledge this.
When we downcast, we take the most significant bytes and throw them in the trash. What do we consider the most significant bytes? The ones that make the number higher essentially. Since the values are from left to right, where the lower values are on the right, and the higher are on the left, we throw out the 2 far left bytes (00000000 00000010) and we’re left with 00001100 01100100.
Now since there was a bit enabled in those two bytes we threw out, it means we lost some data. Our value was originally 134244, and now it’s a measly 3172.
When we upcast it will simply add zeroed out bytes to what we have. So if we have our 00001100 01100100, upcasting from a short to an int will just yield 00000000 0000000000001100 01100100, leaving our value still at 3172.
Bit Manipulation
We’re finally to the topic title! There are many ways you can manipulate bits for storage, or just adjusting them to suit your needs.
Bitshifting
The first method is bitshifting, which essentially is just moving all the bits over to the left or right. The basic process for shifting a byte is to use the shifting operators, >> and <<. If you have a byte bob = 1; you can shift it to the left by 1 with bob << 1. Since we know the value 1 in bytes is 00000001, and we shift it to the left, then new value is 00000010. Shifting to the right bob >> 1 would return it to it’s original value of 00000001.
You’ll also notice you can use this to quickly double and halve numbers. When we shifted bob to the left, it doubled it’s value to 2. If we did that again, it would be 4. and it halves itself when shifting to the right. This applies as a general rule when shifting to the right and left.
Logical vs Arithmetic Shift
There are two types of shifts, logic and arithmetic. They’re pretty similar and have some specific cases when they’re used. Almost all the time in C# you’re using a logical shift. This means when you shift bob << 1 that the new bit will be 0 resulting in 00000010. However, if this was a arithmetic shift, the new bit is copied from the previous, so this would result in 00000011.
There is really only one case where you will have an arithmetic shift, and this is when your value is signed (having both positive and negative values), and you’re shifting to the right. If you have int betterBob = 255 and you betterBob >> 1, this will be a arithmetic shift. If it was just an unsigned int, it would be a logical shift.
Operators
There are several operators that work with binary to change and adjust them. The >> and << are two such operators.
Example values: A(129) = 10001001, B(170) = 10101010
&: The & symbol can be used to return a comparison where both bits are active. If we look at A and B, we check each bit to see if both are 1, so doing (A & B) would result in 10001000 .
A: 10001001
B: 10101010
(A & B): 10001000
|: The | is used to combine two bytes into one. The result will be equal to if either bit is active. The result of (A | B) would be 10101011, for a combined byte.
A: 10001001
B: 10101010
(A | B): 10101011
^: The ^ is for when a bit is 1 in one byte, but not in the other. In the cast of (A ^ B), the result would end up as 00100011
A: 10001001
B: 10101010
(A ^ B): 00100011
~: The ~ is a negation operator, and it only runs on one byte. It just flips all the values to their opposite.
A: 10001001
~A: 01110110
B: 10101010
~B: 01010101
Where Will I Use This?
There are lots of places bits and bitwise operators are used. They’re super efficient for storing boolean values, you could store 8 bools in a single byte essentially, since all a bool needs is a true or false value. Compression and encryption algorithms use bitwise operators a ton too.
Bitwise operators are also super fast. If you need to double or halve a value, bitwise is your man. You can simply left shift to double or right shift to halve the value. Lots of other areas like graphics programming and such use lots of bitwise operators. There are tons of creative cases you can use bitwise operators.
Support
Are you having trouble with understanding this tutorial? Please feel free to contact me via email at KoseckCory@gmail.com or message me on discord at 7ark#8194.
I would love to get feedback from people so I can add and improve these tutorials overtime. Letting me know what you’re confused about will let me update the tutorials to be more concise and helpful.
If you’re interested in supporting me personally, you can follow me on Twitter or Instagram. If you want to support me financially, I have a Patreon and a Ko-fi.
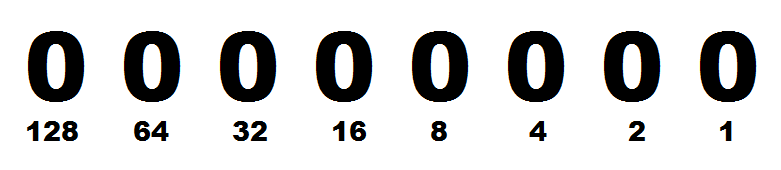
0 comments on “Programming in C#, Part 10: Bit Manipulation”Add yours →